면접에서 자료구조에서 해쉬 테이블을 구현한다 가정했을 때 가장 중요하게 고려해야할 점은 무엇인지에 대한 질문을 받았다. 하지만, 기억에서 잊혀져버린 기본중의 기본을 답하지 못한 것을 반성하며 다시 한번 정리를 해놓으려고 한다.
우선 해쉬 테이블은 (Key, Value) 쌍으로 이루어진 데이터를 저장하는 자료구조이다.
해쉬 테이블은 빠른 검색을 장점으로 내세울 수 있는데, 이것은 내부적으로 버킷을 사용하기 때문이다.
버킷은 데이터 쌍에서 Value 가 저장되는 부분을 말한다.
그럼 Key 는? 이라고 생각할 수 있는데, key 는 해쉬 함수를 통해 index(hash) 로 변환되어 Value 를 가르키게 된다. 즉, Key 만 있다면 즉시 Value 값을 찾아갈 수 있게 되는 것.
때문에 해쉬 테이블 구조의 검색은 O(1) 의 시간복잡도를 갖는다.
핵심은 해쉬 함수로 index(hash) 를 생성한다는 것이다. 그 생성된 index(hash) 는 배열에서의 index(hash) 와 같이 실제 value 를 가르킨다.
자, 근데 이제 문제가 하나 생긴다. 해쉬 함수는 중복된 hash 값을 내보낼 가능성을 내포하고 있다. 즉, 배열로 치면 같은 인덱스가 두번 나오게 될 수 있다는 것. 이를 '충돌' 이라고 말한다.
[여담]
이와 비슷하게 Java 에서의 String 타입의 Hash 값이 실제 value가 다름에도 같은 Hash 가 나오는 경우가 있다.
예로 "0-42L" 과 "0-43-", 두 문자의 값은 서로 다르다.
허나 Hash 값은 같다. 물론, Java String 형의 Hash 생성 구현에 따라 의도 된 것.
이것도 프로그래밍 관점에서 충분히 충돌인 상황이고, 조치를 취해주지 않는다면 Hash 가 같으니 Set 같은데 넣어버리면 중복이라 판단하고 하나는 지워버릴 것이다. (Set 은 중복을 허용하지 않음).
하지만 Java 는 이를 Equal & Hash 로 깔끔하게 해결한다.
'충돌' 은 자료구조의 근간을 뒤흔들 수 있다. 과연 해쉬가 충돌나는 경우 해쉬 테이블은 어떻게 해결을 할까?
1. [분리 연결법]
충돌되어 들어온 해쉬는 그대로 받아주고, 해당 해쉬와 연결된 값을 Linked List 방식으로 이어준다.

위의 그림을 참고하면 아하~ 이런 방식으로 해결했구만! 하고 한눈에 들어올 것이다.
하 지 만, 언제나 그렇든 트레이드 오프가 있는 법.
가정을 해보자. IF, 100개의 해쉬 테이블에 넣고 싶은 데이터의 Key 는 다르다. 하지만, 해쉬 함수를 통해 들어왔더니 전부 다 Hash 값이 같게 나왔다고 쳐보자. 그러면, 위의 그림을 참고삼아서 A의 포인터에서 뒤로 99개가 달려있는 모양이 될 것이다.
아까 이 글의 시작에서 해쉬 테이블은 검색이 빠르다고 했다. 근데? 웬걸 최악의 상황에선 O(N) 이 되어버린다. Linked List 로 순차접근하는 것과 다를게 없어지는 것이다. (물론 언제나 예외는 있다. 극단적이게 예를 들었을 뿐)
그럼 해쉬 테이블의 인생은 여기서 끝난 것인가.. 라고 생각 할 수 있지만 우린 답을 찾을 것이다, 늘 그랬듯이 :)
2. [개방 주소법] 해쉬 테이블로 쓸 공간은 아직 많아! 빈 자리에 집어넣어!
개방 주소법. 이름만 들어선 뭔 뜻인지 이해가 안간다. 하지만 컨셉은 간단하다. 해쉬 테이블 사용한다면 어쨋든 저장 공간을 사용하고 있을 것이다. 해당 할당된 저장 공간이 가득하지 않다면, (마치 하드디스크 10TB 에서 남은 여유공간이 9.8TB 같은..) 그 빈 공간에 때려박으면 되겠네! 라는 컨셉이다.
이 때려박는 컨셉엔 세가지 방식이 있다.
2.1. [선형 탐사법]
간단하다. 기존에 있던 버킷과 충돌이 나면 그 버킷에서부터 순서대로 찾기 시작해서 가장 첫번째로 등장하는 빈 공간의 빈 버킷에 할당해준다.
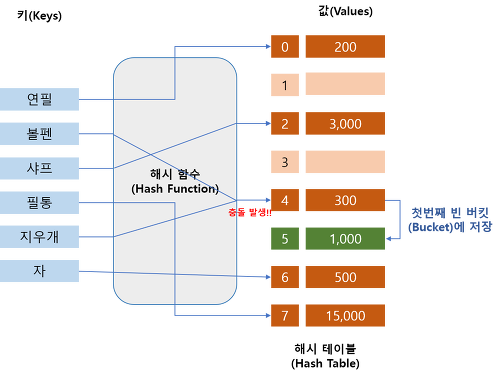
아, 간단 명료하다. 하지만, 이 방식엔 문제가 있었으니. 일차 군집화 문제가 일어난다. 말이 어렵다. 어려운 말은 풀어서 써보자. 일차 군집화의 예는 다음과 같다.
1. 어떤 해쉬 함수를 통해 9 라는 key 가 2 라는 해쉬로 튀어나와서 처음에 저장되었다.
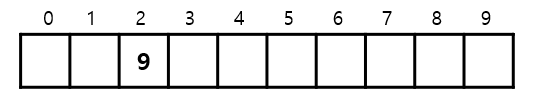
2. 이어서 2 라는 key 가 해쉬 함수를 통해 2 라는 해쉬로 튀어나와서 저장을 하려고 봤더니 그 자리에 9가 있다. 그래서 옆을 보니 비어있다. 저장한다.

3. 이 일이 반복된다. 결국 버킷 2 번지부터 7번지까지 차버렸다.
4. 드디어! 14 라는 key 가 해쉬 함수를 통해 5 라는 해쉬를 받아내었다! 하지만 웬걸....이미 해쉬 2와 충돌나서 옆으로 밀려 저장된 데이터들이 해쉬 5 번지의 주소에 거주하고 있었다.
5. 불행하게도 5 버킷을 받은 14 는 자기가 들어가야할 자리에 들어가지 못한 채 또 하염없이 빈공간을 찾아다닌다.
지옥의 굴레
2.2. [제곱 탐사법]
선형 탐사법과 거의 비슷하지만 바로 근처를 뒤져서 넣는 것에서 벗어났다. 충돌이 난 횟수마다 제곱수를 늘려간다. 즉, 첫번째 충돌은 1의 제곱-> 두번째 충돌은 2의 제곱-> 세번째 충돌은 3의 제곱 번째에 있는 충돌난 녀석을 할당한다.
이 간단하면서 천재같은 발상은 일차 군집화를 해소해준다. 그러나, 결과론적으론 연쇄 충돌 그 자체가 해결된 것이 아니다. 연쇄적으로 충돌이 발생할 가능성은 여전히 열려있다. 이는 이차 군집화라 명명하며 이차 군집화는 다른 새로운 해쉬들의 충돌을 야기하는 것과는 다르게 충돌한 요소가 다시 충돌하는 상황을 말한다.
2.3. [이중 해싱]
완전체가 나왔다. 충돌이 나면 기존의 해쉬 함수가 아닌 다른 해쉬 함수를 통해 또 해슁한다.
정확한 알고리즘 구현에선 해쉬 함수에 쓰일 스탭을 소수를 지정하게 되는데, 소수를 사용하면 나누어 떨어지는 수가 자기자신과 1밖에 없으므로 돌고돌아 같은 녀석이 나올 일이 없도록 만든다.
이러면 충돌 한번만으로 값을 저장할 수 있게된다. 이상적이다.
하지만, 애석하게도 트레이드 오프는 언제는 존재한다. 물론 여느때보다는 좋은 결과를 가져온다.
바로, 단점은 해슁을 두번 거치기에 해슁시 연산 비용이 더 든다는 점이다.
그래서 뭘 써야할까?
우선은 해쉬 함수부터 점검하자. 충돌의 시작은 해쉬 함수를 통하면서부터 이다. 만약 해쉬함수가 웃프게도 x%2 로 되어있었다고 하면 어마어마하게 충돌이 날 것이다. 해쉬 충돌의 선택은 다음을 참고하자. 위에선 세가지의 해결법만 설명했지만 생각보다 많은 충돌해결법이 존재한다.
https://stackoverflow.com/questions/4980757/how-do-hashtables-deal-with-collisions
How do HashTables deal with collisions?
I've heard in my degree classes that a HashTable will place a new entry into the 'next available' bucket if the new Key entry collides with another. How would the HashTable still return the correct
stackoverflow.com
스택오버플로는 언제나 우리의 친구와 같다.
그리고, 해쉬 테이블 저장소의 70% ~ 80% 가 데이터로 차게되면 급격하게 성능이 떨어진다고 한다. 이것은 의도했든 안했든 클러스터링이 모두 되어버린 탓인데. 결국 이렇게 되면 저장소를 늘려야하며 기존 데이터에 대해 싹다 다시 해슁을 해줘야한다.
다음 해쉬 테이블의 더 자세한 부분은 파일처리론에서 들었던 책을 참고하여 작성해볼까 한다.
그래서 어떻게 구현되고, 저장소는 어떻게 늘리며 어떤 모습으로 늘어나는지에 대해서이다.

